😟 Worried You're Starting AS-Level Maths Already Behind?
You're moving into AS-Level Maths — and suddenly realise that many of your classmates studied GCSE Further Maths… but you didn’t.
They’ve seen topics you’ve never touched.
You’re not just starting a new course.
You’re starting at a disadvantage.
😰 You’re Not Alone — But This Feeling Can’t Be Ignored
Without GCSE Further Maths, you might already be feeling:
- ❓ Confused by terms your classmates already know
- 📉 Behind before the lessons have even begun
- 😩 Anxious about falling further behind in class discussions and homework
- 🧱 Blocked by missing foundations in algebra, calculus, or mechanics
None of this is your fault. But without the right support, it can quickly affect your grades and your confidence.
✅ The Solution: Bridging the Gap – GCSE to AS-Level Maths Transition Course
This course is specifically built for students like you — who did NOT study GCSE Further Maths but want to hit the ground running in AS-Level Maths.
It’s your shortcut to levelling the playing field.
What You’ll Get:
📘 A Complete Bridging Booklet
Covers all essential Further Maths topics you should have seen before starting AS-Level Maths.
🎥 Step-by-Step Video Tutorials
Pre-recorded, expert-led walkthroughs to help you fill in the booklet and truly understand each concept.
📝 Interactive Notes
Not passive reading — you're actively working as you learn.
🧠 Topic-by-Topic Practice Questions
Reinforce your understanding and test your progress as you go.
✅ Worked Solutions Booklet
Check every answer with clear, fully explained solutions.
⚡ Instant Access
Download and begin immediately after purchase — no delays, no waiting.
📅 Flexible, Self-Paced Learning
Work at your own pace, on your own schedule, with no pressure.
📚 Topics Covered Include:
🔢 Pure Maths
- Algebra (Triples, Factorising, Quadratics, Algebraic Fractions)
- Differentiation & Integration
- Trigonometry & Inequalities
- Logarithms
⚙️ Applied Maths (Mechanics & Stats)
- Kinematics, Newton's Laws, Vectors
- Mean & Standard Deviation
…and more — everything needed for a strong AS-Level foundation.
🧑🏫 Why This Course Works
✔️ Created by a Qualified A-Level Maths Teacher
Knows exactly where students struggle — and how to fix it.
✔️ Focused on the Gaps
Targets the exact topics you missed by not taking Further Maths.
✔️ Builds Confidence and Closes the Gap Fast
You won’t just catch up — you’ll feel ahead.
🗣️ What Our Students Say:
"Having not done GCSE Further Maths, I was honestly worried about starting AS-Level Maths, especially since it felt like everyone else already knew topics and I didn't! This course helped me so much. I would ask my teacher what topic we’d be covering next in class, then watch the videos on that topic before we started it. It made a massive difference, meaning I wasn’t confused by new terms or feeling behind. The explanations and video tutorials gave me the confidence to take part in class and do my homework without feeling lost. It really turned what could have been a stressful start into something I felt ready for, and I genuinely think it gave me a fair chance to do well in AS Maths."
-Katie, Year 13, Ballyclare
"I watched the videos and completed the notes and questions in August and early September as I wanted to get a head start, but I also relied on the course for revision for quite a few topics on AS1 and AS2 exams. I found myself going back over the videos again and again because so many topics in AS Maths are basically the same as what’s on GCSE Further Maths, which I hadn’t covered. The course made it so much easier to understand everything properly and get ready for my exams. If you’re feeling behind because you didn’t do Further Maths, I’d definitely recommend it."
-Graham, Portadown
🎓 You Deserve a Fair Start
Don’t begin your AS-Level journey feeling behind or overwhelmed.
Bridge the gap now, and step into class with confidence, clarity, and the tools to thrive.
🎯 Click below to access the full course and get started today.
📩 Have questions? Email us at:
Prepare for AS-Level Maths with our Bridging the Gap course, specifically designed for students who did not study GCSE Further Maths. This course bridges the gap between GCSE Maths and AS-Level Maths, ensuring you start on a level playing field. Our comprehensive course offers:
- A GCSE to AS-Level Maths Bridging Course booklet covering all essential topics from GCSE Further Maths that are relevant for AS-Level Maths.
- Detailed examples with space for students to fill in solutions, facilitated by pre-recorded video tutorials.
- Questions throughout the workbook on each topic to test understanding.
- A separate downloadable resource with worked solutions to all workbook questions.
- Instant access to all materials upon purchase. Once you have purchased your course click 'Return to seller' and your purchase should be there for you to download to your device. Please download and save to your device at that stage.
Our course is perfect for students who want to ensure a smooth transition from GCSE to AS-Level Maths, covering all the fundamental topics necessary for success.
Key Benefits
- Comprehensive Coverage: Bridging course booklet covers essential GCSE Further Maths topics needed for AS-Level Maths.
- Interactive Learning: Fill-in-the-blank notes booklet and guided video tutorials enhance understanding.
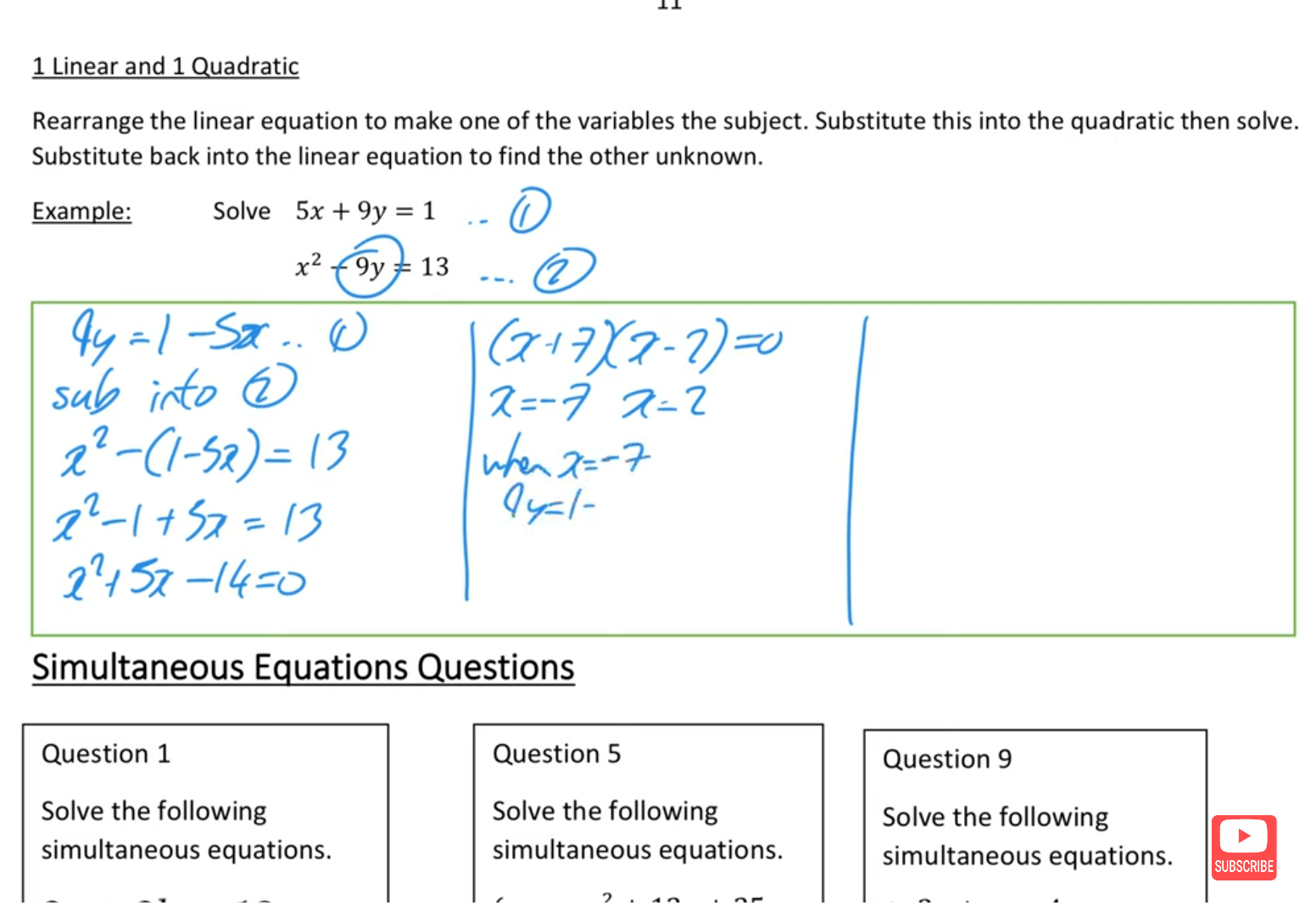
- Test Understanding: Workbook includes questions on each topic to test your knowledge.
- Worked Solutions: Separate resource provides detailed solutions to all workbook questions.


- Instant Access: Get immediate access to all materials upon purchase. Once you have purchased your course click 'Return to seller' and your purchase should be there for you to download to your device. Please download and save to your device at that stage.
- Flexible Study: Learn at your own pace with pre-recorded tutorials.
Call to Action
Ready to bridge the gap and excel in AS-Level Maths? Purchase our Bridging the Gap course today and start your journey to academic success!
More Detail
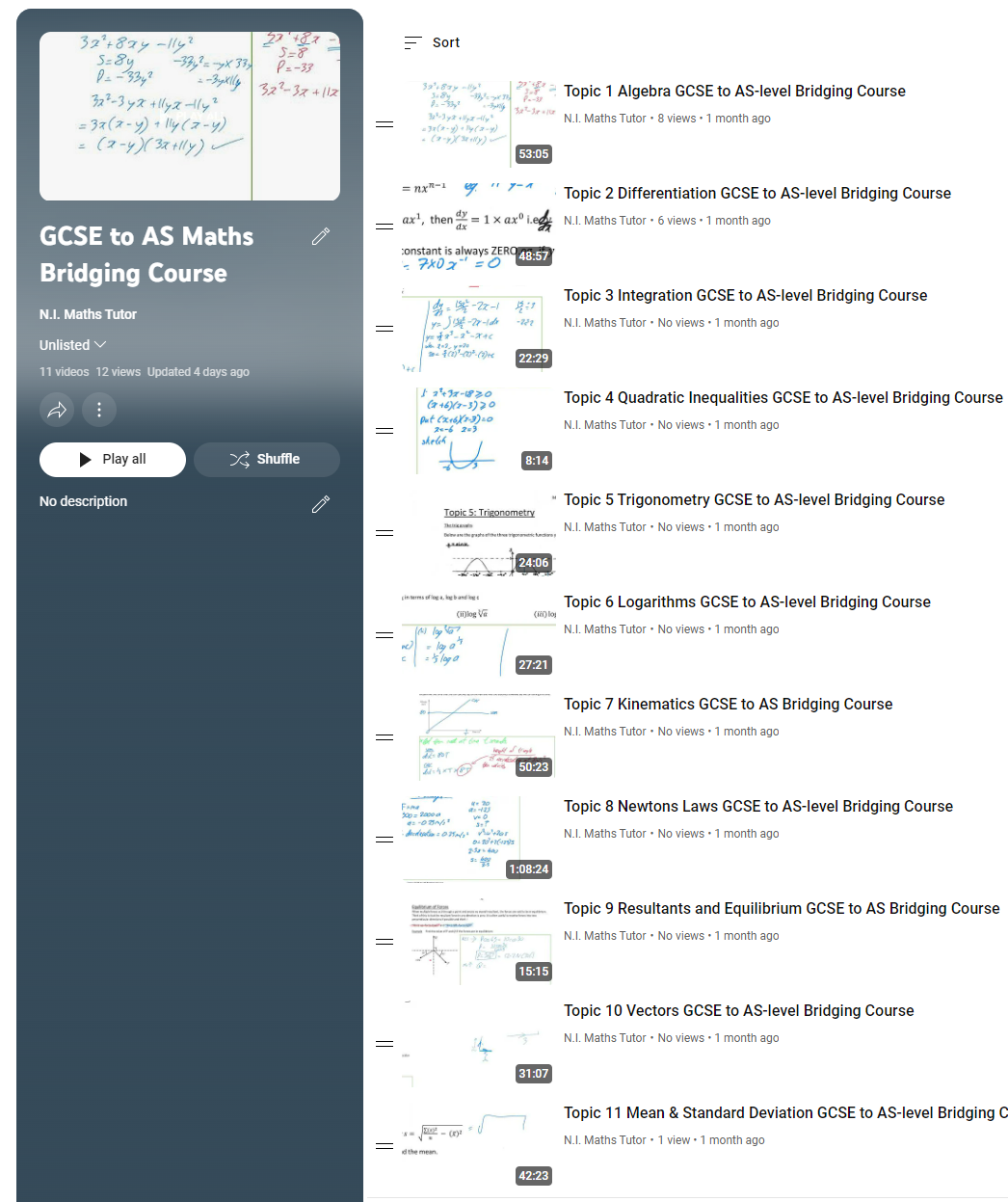
Topics Covered
Pure Mathematics
Topic 1: Algebra
- Multiplying Triple Brackets
- Factorising
- Algebraic Fractions
- Solving Quadratics
- Simultaneous Equations
- Completing the Square
Topic 2: Differentiation
- Gradient of a Curve
- Second Derivative, Stationary Points, and Sketching
- Tangents and Normals
- Maximum and Minimum Problems
Topic 3: Integration
- Indefinite Integration
- Definite Integration
- Using Integration to Find an Area
Topic 4: Linear and Quadratic Inequalities
- Solving Linear Inequalities
- Solving Quadratic Inequalities
Topic 5: Trigonometry
- CAST Diagrams and Solving Trig Equations
- Quadratic Trig Equations
- Adjusting the Range
Topic 6: Logarithms
- Laws of Logs
- Writing Logs in Terms of Other Numbers
- Solving Index Equations
Applied Mathematics (Mechanics and Statistics)
Topic 7: Kinematics
- Velocity-Time Graphs
- Two Body Problems
- Constant Acceleration Formulae
- Motion Under Gravity
Topic 8: Newton’s Laws of Motion
- Resolving Forces
- Inclined Planes
- Friction and Limiting Equilibrium
- Connected Particles
Topic 9: Resultant of Forces and Equilibrium
- Resultants
- Equilibrium of Forces
Topic 10: Vectors
- Magnitude and direction of a Vector
- Vectors in Mechanics
Topic 11: Mean and Standard Deviation
- Types of Data and Grouping Data
- Mean and Standard Deviation from a Frequency Distribution
- Combining and Scaling Sets of Data
How It Works
Video Tutorials: Each topic is delivered through engaging video tutorials. You can watch these at your own pace, allowing you to learn in a way that suits you best. The tutorials are designed to help you fill in the GCSE to AS-Level Workbook provided as part of the course materials.
Practice Questions: To reinforce your learning, the course includes a series of questions related to each topic. These questions are designed to test your understanding and ensure you are fully prepared for AS-level Maths.
Why Choose Us?
- Expert Instruction: Learn from a seasoned Mathematics teacher with years of experience in guiding students through their A-level journey.
- Flexible Learning: Access the video tutorials and materials at any time, allowing you to learn at your own pace.
Ready to Get Started?
Ensure you're fully prepared to excel in AS-level Mathematics. Enrol now and take the first step towards a successful academic future!
For more information, please contact us at
Don't miss out on this opportunity to bridge the gap and achieve your full potential in A-level Maths.
Click the link below to Purchase now!








